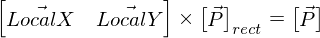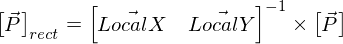The challenge was to decide whether a 2D point is within a given distance to a rectangle, which might be rotated. I first solved this in C# but then decided to remake it in Python to graph/test my solution.
Initial Thoughts
The rectangle is described by center position, dimensions, and the local X and Y axes which describe rotation. For no rotation, these are (1,0) and (0,1) respectively. A 45 degree rotation is represented by (1,1), (-1,1) for localX and localY.
Immediately, I considered distance equations involving points and lines. Naively, I could test the point to see if it’s within all 4 line segments of the rectangle, and if it isn’t, find the distance to the edges and corners. This seemed unwieldy so I considered the fact that the problem is simpler if the rectangle is not rotated and is centered at origin. Thus I set out rewind the rectangle’s transformations by applying them in reverse to the point (e.g if the rect was rotated 10 degrees CCW, rotate the point 10 CW). I found this transformation by finding the change of basis matrix, which, simply enough, is just the column vectors of the rectangle’s local X and Y axes.
Reversing this is as simple as inverting the matrix and applying it.
After finding the point relative to the rectangle, I took the absolute value of the point’s coordinates. If the point was at (-20,-10), the distance is the same as if it were (20,10). This greatly simplifies the logic. The rest of the code is testing whether the point is inside, to the right, above, or right & above, of the rectangle. Finding the distance in each case is trivial.
Great, so the initial plots look correct for a normal rectangles. My plan to visualize it worked it, meaning I can see many results at once. The third picture shows the points close to an infinitely small rectangle. As predicted, it’s a circle. Lastly, I tried changing the rectangle’s axes so they weren’t 90 degrees from each other. This results in a parallelogram, as seen in the last image. Success!
My code is a little more complex than necessary since I wanted practice in documentation, to use Numpy for matrix inversion, and proper command line support. My initial implementation in C# didn’t use external libraries and was much more efficient, but that wasn’t a goal for this version.